Build log: The "Crazy Circuit Conundrum" for Midnight Sun CTF
My friend Calle Svensson (@ZetaTwo) recently arranged the Midnight Sun CTF, and wanted to include a challenge about reverse-engineering a custom low-level logic circuit. He asked me to help, since I have tinkered with just that a bunch lately, and I was very happy to. The result of this became the “Crazy Circuit Conundrum” challenge, and in this post I’ll tell the story of this challenge came to be. This obviously included a bunch of soldering and PCB design, but also some brief Boolean logic reasoning and algorithm design, and of course some mistakes.
My hope is that this will give you some insight into how building custom circuits works and, if you’re not familiar with these topics, show that although the end results may look complicated, the individual steps along the way are actually pretty simple — these are all things you could learn from scratch with a few months of practice.
All schematics and scripts mentioned in this post are available on GitHub.
Step 1: A first draft
The initial prompt I got from Calle was this (translated from Swedish):
Hey! I have an idea for a CTF challenge for the finals we’re arranging
a circuit with some low level logic and some DIP switches and a button and a light
if the DIP switches are in the right position the light lights up when you press the button
We discussed this a little further, considering things like maybe including some memory component that could make order of operations significant, but in the end we settled on making it a rather simple stateless Boolean function. So into KiCad I went and started sketching up a first draft.
The first draft was a very simple circuit — just 16 circuit breakers each connected to an XOR gate whose other input is hardwired to 1 or 0, all those XOR outputs in turn connected to a 16-input NOR gate, and that NOR output controlling a transistor that controls an LED. The NOR gate would output 1 only if all of the XOR gates output 0, which would happen only if the 16 breakers are in the same configuration as the hardwired inputs.
So that’s all well and good, but this wouldn’t be much of a challenge to reverse-engineer — the answer is right there in the hardwired inputs. So we decided to make it a little more complicated.
Step 2: Shuffle the expression
Calle suggested that some inputs could affect multiple gates, and I that we could do a more convoluted Boolean function. These two gave me the idea of using a script to randomly generate the function to use. The script and its revisions can be found on GitHub. Here’s some output from the first version:
$ ./generate-formula.py
and( (i11 and i8), (i2 and i5), (i12 and i4), (i1 and i11), (i3 nand i12), (i5 nand i3), (i10 nand i1), (i6 nand i13), (i13 nor i16), (i7 nor i10), (i14 nor i2), (i16 nor i14), (i4 xor i6), (i15 xor i15), (i9 xor i7), (i8 xor i9) )
and: 4
or: 0
xor: 4
nor: 4
nand: 4
self: 1
Calle then reminded me that the solution to this might not be unique, and it is indeed not. So how do we guarantee that the function we generate has exactly one input for which it evaluates to 1? Time for some Boolean logic reasoning!
To keep things simple, I decided to keep the structure of the function as a simple AND conjunction of two-term operations, where each input appears twice. This overall AND conjunction will evaluate to 1 if and only if all of its inputs are 1 — that is the definition of the AND function, after all. So how do we make sure that each of the conjunction terms is 1 for exactly one input?
Consider the truth table for the AND, OR, XOR, NOR and NAND operators:
| a | b | a AND b | a OR b | a XOR b | a NOR b | a NAND b |
|---------|---------|---------|--------|---------|---------|----------|
| 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 |
Notice that only the AND and NOR columns contain exactly one 1, meaning there is
only one input for which they are 1. Indeed, if a XOR b = 1, then also
¬a XOR ¬b = 1, so an individual term with a OR, XOR or NAND operator is 1 for
more than one input. It’s still possible to make the overall function have a
unique input that maps to 1, but it would require cross-conditions between the
terms. But if we use only the AND and NOR operators in our conjunction terms,
then each term will be 1 for exactly one input, and we’re guaranteed that the
whole conjunction will be 1 for exactly one input.
Notice that applying the NOT operator ¬ to either a or b does not affect the
number of 1s in the columns — all it does is rearrange the rows of the table
— which means we can sprinkle NOTs onto the inputs without affecting the
uniqueness of the solution.
Armed with this knowledge I updated the generator script to only generate conjunctions with a unique solution. I also got some help from Calle who gave me some snippets of z3 code for solving the equation, which I extended to verifying that the solution is in fact unique. Here’s an example output from the final version of the script:
And(And(Not(dip_2), Not(dip_6)),
And(Not(dip_1), dip_10),
Not(Or(dip_2, dip_4)),
Not(Or(Not(dip_5), dip_6)),
And(dip_10, Not(dip_13)),
And(dip_12, dip_14),
Not(Or(Not(dip_5), dip_0)),
Not(Or(dip_4, Not(dip_3))),
Not(Or(dip_7, Not(dip_9))),
And(Not(dip_11), dip_12),
Not(Or(dip_8, dip_1)),
Not(Or(Not(dip_3), dip_15)),
And(Not(dip_15), Not(dip_0)),
And(dip_14, Not(dip_8)),
And(Not(dip_11), dip_9),
Not(Or(dip_13, dip_7)))
[dip_15 = False,
dip_8 = False,
dip_11 = False,
dip_9 = True,
dip_7 = False,
dip_3 = True,
dip_0 = False,
dip_14 = True,
dip_12 = True,
dip_13 = False,
dip_5 = True,
dip_4 = False,
dip_10 = True,
dip_1 = False,
dip_6 = False,
dip_2 = False]
Solution is unique!
This first prints the z3 model of the function, then an input for which it evaluates to 1, and finally verifies that this solution is unique. With that, I was ready to implement this function in an electronic circuit — but first, there was an itch I had to scratch…
Step 2b: Improve the script
The first few versions of the script would simply generate a random set of terms for the conjunction, check if it has a unique solution and keep retrying until it found one that did. This worked well enough but was pretty slow, and while improving it wasn’t really necessary for the sake of getting a usable function out of it, I enjoy the craft.
So, the reason why the first script took so long to run was because it just blindly tried combinations of conjunctions until it found one that works. The vast majority of the possibilities it tries will have no or more than one solution — but we can be a bit smarter about which possibilities we try.
The final version of the script starts from an empty conjunction and uses dynamic programming to recursively expand the conjunction with one term at a time, making sure to not pick a term that will immediately make the function unsolvable. For example, if we have the function
AND[AND(i3, NOT(i5)), NOR(i5, i3)]
then we know that if we pick AND(NOT(i3), i13) as the next term, then the
function can never evaluate to 1 since the input i3 must be both 0 and 1 at
the same time.
So, we eliminate those possibilities as we go. If at any time we eliminate all the possibilities, meaning it’s not possible to add another term, then by the recursive nature of the function we simply back up and try other possibilities for the previous choices of terms.
This greatly reduces the number of bad combinations we need to try before finding a good one, since we can eliminate entire regions of the space at a time instead of just individual points. As a result, the script finishes in about a second instead of a couple of minutes. Itch successfully scratched.
Step 3: Schematic
Now that I had a Boolean function to use, it was time to implement it in hardware. The original plan was to do this with hand-drawn wires on an off-the-shelf experiment board, since there was little time before the contest. Calle later told me that Eurocircuits actually offer PCB manufacture and delivery in a couple of days, so in the end we had a PCB made as well, but I’ll begin with the creation of the hand-made prototype. This, of course, began with a schematic.
The first step was to pick the components to use, so I know what I need to lay out in the schematic. I had already browsed around a bit and noticed that many AND and NOR ICs come in packages with 4 pairs of inputs, so I designed the generator script to generate 8 AND and 8 NOR terms. That meant I’d need 2 AND ICs and 2 NOR ICs.
By inspecting the formula I chose I could also determine that I would need 15 NOT gates. These seem to commonly come in packages of 6 gates, so that means I need 3 of those ICs.
Finally, I needed a big AND gate to combine all 16 terms through. I didn’t find
any 16-input AND gates, but I did find an 8-input one. Since AND(a, b, c, d) =
AND(AND(a, b), AND(c, d)), I could simply combine 2 of those with a 2-input
AND gate built from 2 discrete MOSFETs.
So with that I went to my local retailer Electrokit, searched for “AND gate” etc., and simply picked the cheapest DIP ICs I could find that matched the descriptions above. I ended up with this list of components:
- 3x 74HCT04 DIP-14 Hex inverter
- 2x 74HCT08 DIP-14 Quad 2-input AND gate
- 2x 4001B DIP-14 Quad 2-Input NOR Gate
- 2x 4068B DIP-14 8-Input NAND/AND Gate
That’s most of what I needed to start wiring up components on the schematic, so back into KiCad I went. KiCad’s symbolic network labels came in very handy here to keep the cross-connections manageable.
Since the final AND ended up being broken up into two parts, I decided to add an additional LED for each half just for fun. It might also serve as a lagom confusing red herring that could make you think you have half the solution right, even though that’s not actually the case.
The J1 component in this schematic is a USB micro-B connector for power supply. The hand-built circuit didn’t have this or the C1 smoothing capacitor — it just had a pair of standard 2.54 mm pitch header pins to connect power and ground to — but the final PCB version does. The two parallel resistors R19 and R20 are purely for symmetry to make the PCB layout pretty.
With that, it was time to order components and eventually start soldering!
Step 4: Prototype board
A picture speaks a thousand words, as they say, so here comes a flurry of photos from the build process.
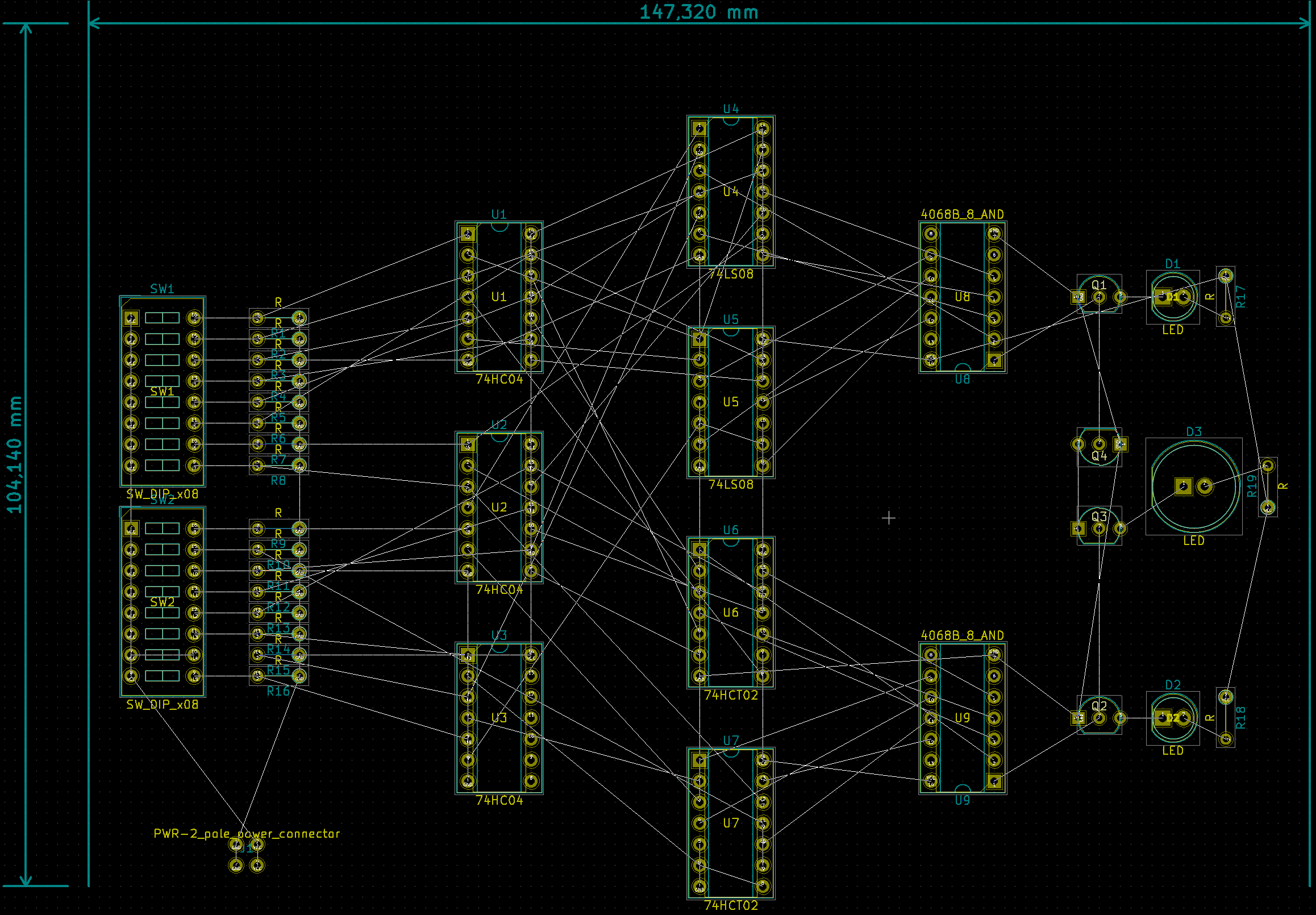
Figure 3: Rough layout of component footprints in KiCad, where I get both a feel for how large an experiment board I need, and a rough overview of which connections will need to go where.
Left: The whole layout. Right: Example of using KiCad to highlight pads that are on the same network, i.e., connected to each other.
Throughout the process I continued double-checking the connections with the continuity probe, making sure that the pads connected in the schematic were in fact connected on the board and not accidentally connected to their neighbors (see Figure 3). As a direct result, between Figure 6 and Figure 7 I discovered an error: I had connected one of the first yellow wires to the wrong IC pin at one end. I’m glad I caught that here and not later in the process. “Check twice, solder once”, as Boldport advises on The Tap.
And there you have it, the finished prototype board!
As you can probably imagine, the vast majority of the time spent on this assembly went into cutting, stripping and attaching those I-don’t-actually-know-how-many wires. I estimate that that alone took around 8 hours in total, while the entirety of the assembly took about 10-12 hours in total. This is, in my opinion, one of the biggest reasons to have custom PCBs made — just so you don’t have to deal with all those wires and the inevitable mistakes you’ll make in connecting them.
Anyway, with this confirmation that the circuit works, we proceeded to order a custom PCB for it.
Step 5: Custom PCB
I had initially assumed that 2 weeks was too short a lead time to have a PCB manufactured, but it turns out Eurocircuits offer PCB manufacturing with lead times as short as 1 day! Of course the price for this service is much higher than for longer lead times, but that was apparently not a hindrance in this case. So I placed the order on Sunday night, and the board was delivered the following Thursday.
Eurocircuits also offer a PCB service they call “NAKED proto”, which makes naked prototype boards with no soldermask or silkskreen, but at a lower price. No soldermask or silkscreen means that all the copper on all tracks and zones is directly exposed. This actually turns out to be an advantage for us, since we want the tracks to be easy to see and follow visually.
Step 5a: Routing tracks
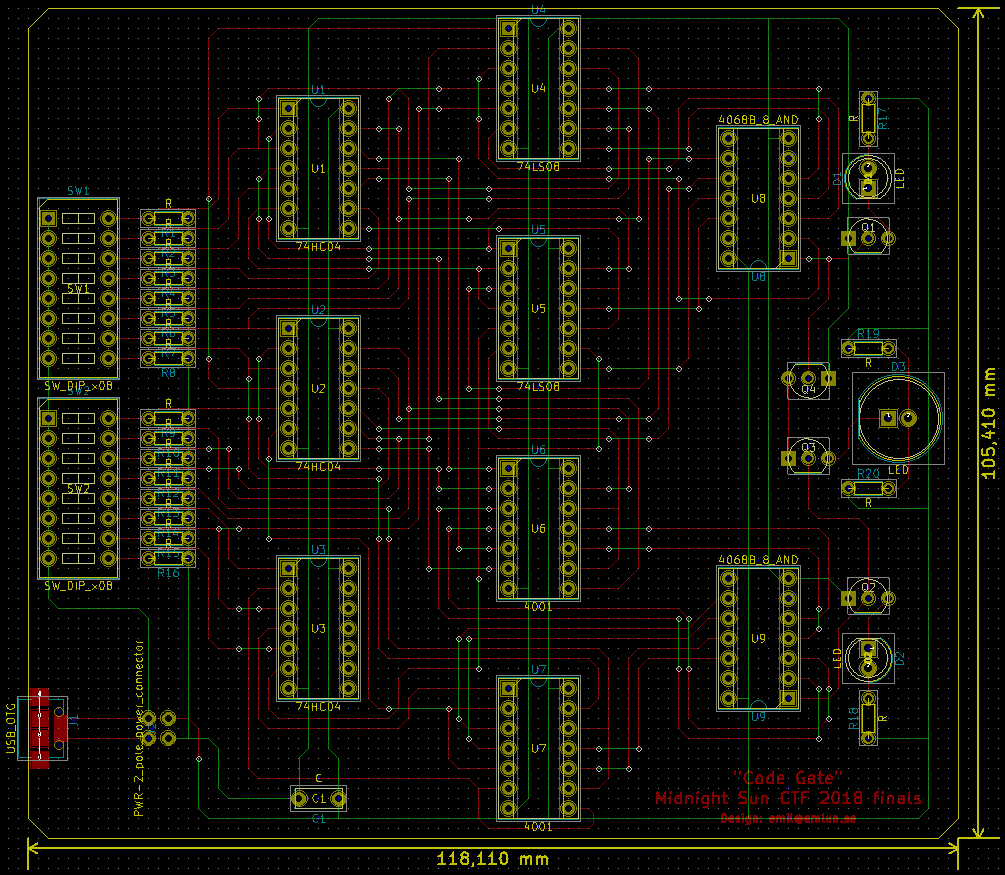
Anyway, to get a PCB manufactured you need a schematic. I had much of it done already since I’d already designed the circuit and roughly laid out the component footprints as seen in Figure 3, but the nontrivial task of routing all the tracks remained. This was quite messy — as you can see in Figure 7 — since that was after all one of the design goals. It took a few hours to do, working through several iterations of footprint placements and routing strategies, but I eventually got to a place I felt happy with. I tried to keep as much of the tracks as possible on the top side of the board, to make it easier to “read”, and I also tried to make the tracks on the backside as predictable as possible in where they go.
One interesting thing to note about this schematic is that there are no zones in it. It’s common for PCB designs to have large zones of copper on both sides of the board, which you assign to a particular network and which then get automatically connected to all pads on that network without needing individual tracks. For example, my previous boards have had a VCC zone covering the entire top side and a GND zone covering the entire bottom, so that I don’t need to worry about the (on my boards, many) connections to power and ground. However, since this design would be printed on a “naked” PCB with no soldermask, having large exposed copper zones would be a major short circuit hazard, so for this design I routed those connections manually instead. This probably made the circuit a little easier to read as well.
To finish things off, I like adding some text to my boards that describes what it is and who made it. I like doing this with copper instead of silkscreen, to make it both a little prettier and hopefully more resistant to wear. This is probably an idea I’ve unconsciously picked up from the beautiful boards I regularly get from Boldport Club. To accomplish this, I add a pair of identical text boxes to both the F.Cu (front copper) and F.Mask (front soldermask) schematic layers. The former makes sure that this copper doesn’t connect to anything carrying current, and the latter makes sure that the copper is exposed and visible — although that wasn’t actually necessary for this particular board, since it doesn’t have a soldermask layer.
I named the board “Code Gate” — mostly as an homage to Android: Netrunner, but also because it’s a “combination lock” made up of logic gates. Calle independently named it “Crazy Circuit Conundrum”, which I also like a lot, but didn’t know about at the time — this was late at night and I needed to get the order submitted for manufacturing, and I hadn’t thought to ask about naming before.
Step 5b: Additional components
As noted earlier, I also added two additional components for the PCB version: a USB micro-B connector for supplying power, and a smoothing capacitor.
I don’t really know how to use or choose a smoothing capacitor — I knew it’s used to smooth out sudden jumps in voltage, like when connecting or disconnecting a power source, but that’s about it — so I turned to the friendly souls in Boldport Club for assistance. Apparently you’re supposed to have one smoothing cap for each IC, and as close to it as possible — but since the prototype board worked just fine without any at all, I figured just one should do just fine. This circuit doesn’t need to survive a long time, and we’re not using any high voltages or high-frequency signals or anything, so I prefer to keep it simple. I was also told that 100 nF is a good go-to value for smoothing capacitors, so I just went with that, and some quick reading on Wikipedia told me that out of the many different kinds of capacitors there are, ceramic ones are typically used as smoothing caps. Which is nice, since they’re also really cheap.
The USB connector was pretty straightforward — I just needed to look up which pins are power and ground, order a connector and plop down a footprint on the schematic… except the KiCad libraries don’t have a USB micro-b connector footprint that looked compatible with the drawing in the datasheet for the connector sold by Electrokit. So, I needed to add one! This is actually a lot easier than it may sound - starting from the closest existing footprint in the libraries, it was just a matter of looking at the datasheet and adjusting the dimensions and spacings until everything agreed.
Step 5c: Placing the order
With the schematic complete, all that was left was to submit the order for the PCB to Eurocircuits and order the components to solder onto it. It turns out Eurocircuits allows you to simply submit a KiCad project file and they’ll take care of the rest, which is much more convenient than having to plot Gerber and drill files and send those in.
So submitting the order was quick and easy. Eurocircuits then impressed me by apparently performing manual review of the design - and they found something strange in it: in my USB connector footprint (see Figure 12) I had used a pair of pads to create the drill holes for the alignment pins, and set the diameter of the soldermask hole to equal the diameter of the hole. But since I used a pad to mark this, that meant this hole was listed as a plated through-hole drill for soldering a component in, and not a non-plated mounting hole. The Eurocircuits engineers noticed this and the fact that I hadn’t left any copper exposed to solder to, and — since they could clearly see these were meant to be non-plated mounting holes — just fixed it for me. That’s some really good service right there!
So with the PCB ordered, here’s the bill of the remaining materials I ordered from Electrokit:
| Item | Qty | Tot. price, SEK |
|---|---|---|
| USB micro-B kontakt SMD | 1 | 11.00 |
| 74HCT08 DIP-14 Quad 2-input AND gate | 2 | 7.80 |
| 4001B DIP-14 Quad 2-Input NOR Gate | 2 | 10.00 |
| 74HCT04 DIP-14 Hex inverter | 3 | 15.00 |
| 4068B DIP-14 8-Input NAND/AND Gate | 2 | 11.25 |
| LED 10mm grön klar 10000mcd | 1 | 4.69 |
| DIL-hållare 14-pin | 9 | 15.75 |
| LED blå 5mm 3500mcd klar 25gr | 2 | 10.00 |
| 2N7000 TO-92 N-ch 60V 200mA | 4 | 8.00 |
| DIP switch 8-pol | 2 | 16.00 |
| Keramisk MLCC 100nF 50V X7R 5mm | 1 | 4.00 |
| Motstånd kolfilm 0.25W 10kohm (10k) | 25 | 9.38 |
| Motstånd kolfilm 0.25W 1kohm (1k) | 4 | 4.00 |
| Total | 126.86 |
In case you’re wondering why I ordered 25 10 kΩ resistors when there’s only 16 pull-down resistors in the schematic: the reason for that is that the bulk discount means the total price of 25 resistors was actually lower than the total price of 16 resistors. I’m sure I’ll find a use for them eventually.
Step 6: Assembling the PCB
We’re getting close to the end! All that was left now was to solder the components to the PCB. This took a lot less time than assembling the prototype board, since all the connections were already done and all I had to do was shove the components in and solder the pins. I think the entire assembly took about 1 to 2 hours in total.
The only snag I hit was that I ordered the wrong size resistors — apparently I didn’t check that the footprints I used agreed with the actual size of the things. Luckily I had a bunch of smaller resistors at home already. The ones I’d planned to use were 10 kΩ pull-down resistors for the inputs and 1 kΩ resistors for the LEDs, but I ended up using 1 MΩ for the pull-downs and 10 kΩ for the LEDs because that’s what I had at home. It doesn’t really matter for the pull-downs, since timing and stuff like that is irrelevant to this project, and the LEDs just ended up a little dimmer (but still pretty bright) than planned.
Apparently the USB connector broke off halfway through the contest. I don’t know what I could have done to prevent that, other than build the thing into a chassis that could provide a ceiling to prevent the connector from twisting.
Other than that, the assembly went smoothly and the circuit worked just fine on the first try. I would like to say something more here, but I really don’t have much else to say. Other than that computer-aided design (CAD) is a powerful thing!
Epilogue
So there you have it: that’s what went into the making of the “Crazy Circuit Conundrum” challenge. Thanks a lot for reading! I’d also like to thank Calle for inviting me to help with the contest, and Boldport Club for answering my n00b questions about smoothing capacitors.
If you’d like to contact me with any comments or questions of any kind, feel free to e-mail me or ask Calle.
If you have some familiarity with electronics and want to learn how to make your own PCBs, I can recommend the official KiCad getting started guide. Follow along with the tutorial project and you’ll pick up the basic core concepts, and from there you can start exploring on your own once you have a basis to stand on. Once you feel ready to actually have something manufactured, I can recommend PCBs.io for the simple process and affordable prices. There are also other low price services like OSH Park and Dirty PCBs, but I haven’t tried them.
Once again, thank you for reading!