Advent of Code 2019 in 130 ms: day 18

Day 18: Many-Worlds Interpretation

Challenge 18 also took quite a bit of effort to optimize. Basically, it’s a maze optimization problem, but with the added twist that you need to collect keys to open doors, and in part 2 you’re exploring 4 partitions of the map in parallel.

My solution runs in 11 ms, and gets its performance from a lazily constructed abstracted world map, a custom collection type storing keys in a bit field, and a compact representation for detecting duplicate states.

The abstract graph

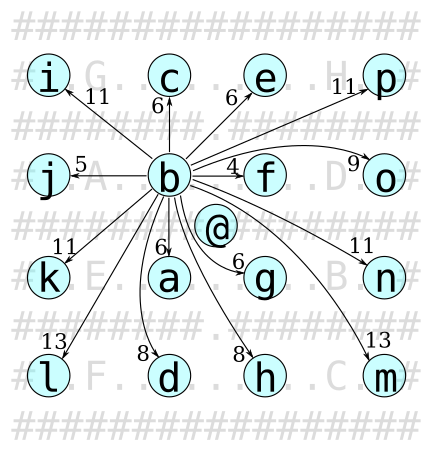
The abstracted world map is a graph of shortest paths between keys, as shown in figure 8. This greatly reduces the size of the search space compared to the basic world map, as one “step” in the graph can represent hundreds of steps on the actual map.

This abstract map assumes all doors are open, but each connection records which doors and keys it passes. This way we can reuse the map regardless of what keys we have currently collected. In code, the graph is represented as a hash map, mapping points to vectors of route objects. A route object contains a length, the end point, and the keys and doors along the path. For example, the map for figure 8 has an entry mapping (6, 3) to a vector containing the route

{
  to: (1, 7),
  length: 13,
  keys: ['l'],
  doors: ['F']
}

For maximum performance, this map is built lazily on demand the first time we need to navigate from each point. This is done by a simple exhaustive breadth-first search (BFS) through the basic map.

Using this higher-level map, the real work is done using Dijkstra’s algorithm to find the shortest path that visits all keys. This is similar to a basic BFS, but where steps can have different lengths. Like BFS, it uses a queue of locations to explore, but unlike basic BFS, it is a priority queue which sorts the locations by the total number of steps taken. This ensures that the currently shortest path is always processed first, even if it has more (but individually shorter) steps than other paths.

The states for this Dijkstra search have a current position, a set of collected keys, and a total number of steps taken. We initialize the queue with a state at the starting position with no keys collected. For each state in the queue, we use the abstract map to get the list of routes from the current position, and generate a new state for each route which contains keys we have not already collected, and does not pass any doors for which the current state hasn’t yet collected the keys. Figure 9 illustrates how new states are generated by filtering the routes in the abstract map.

An important note here is that the abstract map includes routes that pass more than one key. For a long time, my solution only allowed one key per route, my thinking being that this reduces the branching factor; when I removed this restriction, my runtime was reduced by 80%.

Key sets as bit fields

The abstract map is the main algorithmic trick, but for it to run quickly there’s a fair bit of tricks to improve implementation efficiency. The algorithm involves a lot of comparing sets of keys to make sure we don’t explore paths we don’t have the keys for, as well as copying sets of keys to new states. This can be made much more efficient by representing key sets as a bit field instead of hash maps. This turns most set operations - union, intersection, subset check, etc. - into a single bitwise AND or OR operation, and copying a set is practically free since it’s stored in a single integer value.

My solution therefore converts the key characters in the input map into key IDs being powers of two, and represents key sets as bitwise OR combinations of key IDs, as shown in figure 10. This optimization alone reduces runtime by about 75%.

        z...gfedcba                               z...hgfedcba
        -----------                               ------------
a, A => 0...0000001      {a}                   => 0...00000001
b, B => 0...0000010      {a, b}                => 0...00000011
c, C => 0...0000100      {c, e}                => 0...00010100
d, D => 0...0001000
e, E => 0...0010000      {a, c, e} ∪ {b, c, g} => 0...01010111
f, F => 0...0100000      {a, c, e} ∩ {b, c, g} => 0...00000010
...

Compact duplication keys

A Dijkstra search needs to keep track of which locations it has already found a shorter path for, so that it can discard states from the queue if a shorter path was found after the state was added to the queue. In this case we need to take keys into account for this, so a simple solution is a hash map mapping pairs of (keys collected, position) to the length of shortest path to get there. Again, though, this involves a lot of manipulation of large values. To speed this up, my solution instead uses a hash map of duplication keys to path lengths. The duplication key for a state is the set of collected keys and the position - or positions, for part 2 - packed into a single u128 value as shown in figure 11. This is easy to compute since key sets are already represented as u32 bit fields. This saves about 15% of run time, but does assume that the map is no larger than 4096x4096 tiles.

Keys:            [a  d         n    s uv]
Positions:       [(13, 39), (5, 45), (53, 43), (41, 39)]
Duplication key:

    zyxvutsrqponmlkjihgfedcba
-----------------------------
0...0001101000010000000001001

  y0 = 39      x0 = 13      y1 = 45       x1 = 5
|----------| |----------| |----------| |----------|
000000100111 000000001101 000000101101 000000000101

  y2 = 43      x2 = 53      y3 = 39      x3 = 41
|----------| |----------| |----------| |----------|
000000101011 000000110101 000000100111 000000101001

Part 2

For part 2, we need to explore 4 partitions of the maze in parallel, while keys may unlock doors in other partitions. This turns out to be very easy to incorporate - the basic breadth-first search to build the abstract map doesn’t change at all, and the states of the higher-level Dijkstra search simply have four positions instead of just one, and generate new states from each position. The duplication keys still fit comfortably in a u128 since we’re guaranteed to not have to deal with more than 4 positions - again under the assumption that the maze is at most 4096x4096 tiles. In fact, having a Vec<Point> instead of just a Point in the key for the map of shortest lengths was my motivation for trying the duplication key method.